
本文为原创文章,转载请注明出处!
本文主要是写一下自己在使用Z3约束器来解方程时遇到的坑,失败了好多次才流泪写下这篇教程(好几次都想放弃) 避免大家和我一样浪费时间 百度谷歌了好久 也没找到方法 话说大佬们是不是有什么技巧
z3是由微软公司开发的一个优秀的SMT求解器(其实就是一个定理证明器),它能够检查逻辑表达式的可满足性。我们做CTF逆向题可能会经常用它来解方程。变量类型有整数Int,实数Real(需要得到float型的值时可以用这个),至于数组,就用BitVec好啦
先来说一下简单的使用吧
比如我想求一下a*b=0x24这个方程的解

很明显,这里的解不止一个
这里就是z3的一个特点就是当解有多个的时候只会帮我们求出一个可能的解
如果我们想要拿到需要的解 那就增加约束条件 比如我想要得到当a==2时的解 就像下图所示:

1:确定你的Python版本为2.X(我的是2.7)
2:pipinstall z3或者pipinstall z3-solver是不行的(亲测)
3:必须采用源码安装
下载链接:
https://pypi.org/project/z3-solver/4.5.1.0/#files
我用的是这个版本 可以正常使用 好像有新版本 你自己可以尝试
4:下载对应电脑版本的
我的电脑是win10x64位专业版,所以我选择的是
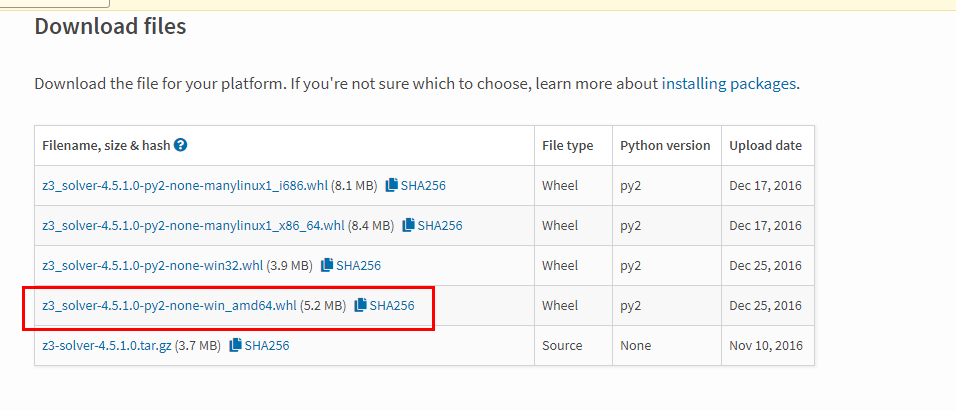
点击就可以下载
5:安装的话直接cmd
(如果你的环境变量配置的是默认Python3的话 记得一定要切换到Python2.x\Scripts)
6:最后输入命令
pipinstall z3_solver-4.5.1.0-py2-none-win_amd64.whl

注意:文件路径,我是直接放在了桌面
以iscc中的一道逆向题为例
先放到我的ubuntu子系统中 file一下 格式file + 文件名
知道是elfx64位文件,于是直接载入IDAx64中,函数不是太多,直接双击左侧main
发现右侧图形模式很明显的可以看到一些关键的字符串,稍加思索就可以知道sub_400766就是关键的函数 jz是关键跳转
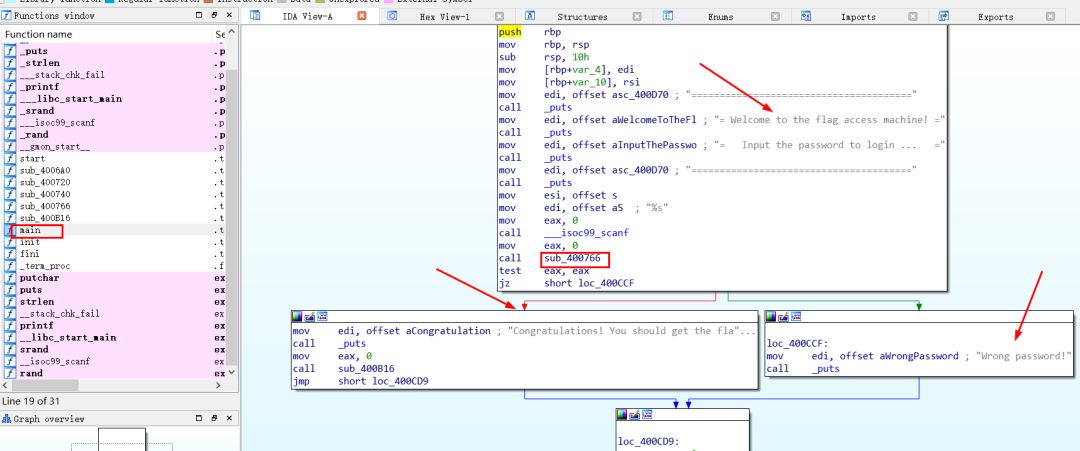
那么我们先F5一下,接着双击函数名
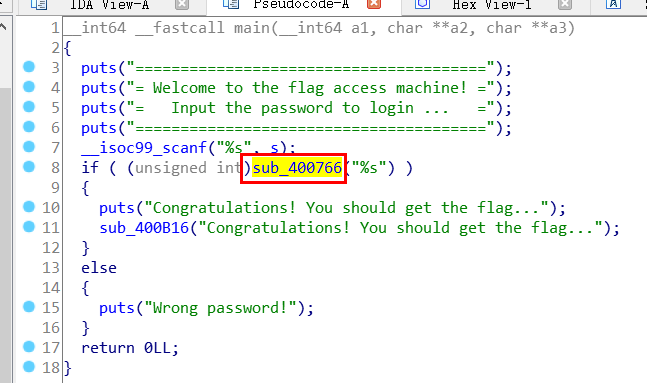
看到有一个长度的判断 还有两个四元一次方程组 等等

但是这样对于新手来说不太好看 那就美化一下
在s头上按Y键 将原来的char s[4] 改为chars[32] 点击OK

将那些让人头大的变量名按N重新命名(x1~x8),就像下图一样
接着右键—Hidecast(隐藏声明),最后变成这个样子

具体计算的时候我们分开来做,先来求解第一个方程组
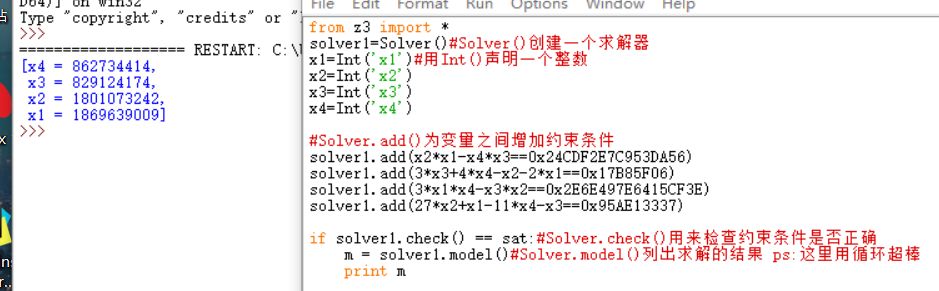
这时候可以得到
[x4= 862734414,
x3= 829124174,
x2= 1801073242,
x1= 1869639009]
接着打算用python求srand的种子还有确定v1,v2,v7,v8,v9,v10,v11,v12的值的
但是不会
我是直接gdb动态调试得到的
v1= 0x16
v2= 0x27
v7= 0x2d
v8= 0x2d
v9= 0x23
v10= 0x29
v11= 0xd
v12= 0x24
有大佬用的C语言解的 我觉得很不错 贴上来
#include<stdio.h>
#include<stdlib.h>
intv1,v2,v7,v8,v9,v10,v11,v12;
intmain(void) {
srand(829124174^ 1801073242 ^ 1869639009 ^ 862734414);
v1 = rand() % 50;
v2 = rand() % 50;
v7 = rand() % 50;
v8 = rand() % 50;
v9 = rand() % 50;
v10 = rand() % 50;
v11 = rand() % 50;
v12 = rand() % 50;
printf("v1=%d \n v2=%d \n V7=%d \n v8=%d \n v9=%d \n v10=%d \n v11=%d \nv12=%d",v1,v2,v7,v8,v9,v10,v11,v12);
return0;
}
接着求解第二个方程组,代码如下
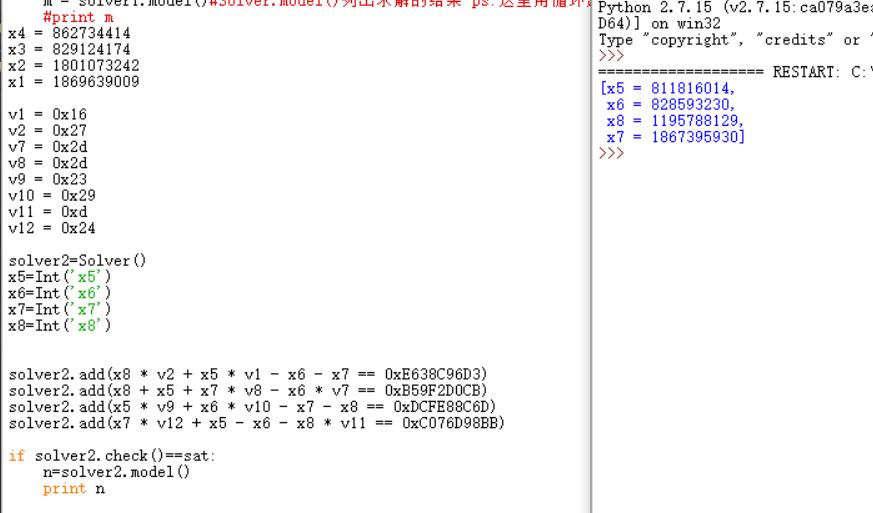
好啦 接下来就简单了
不过还缺一个库libnum(同样只能python2.x安装百度有教程),我还是用kalilinux吧
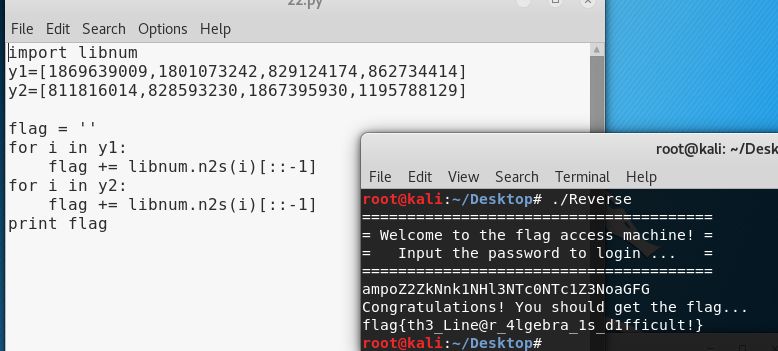
当然这个还不是flag
需要运行 输入得到的ampoZ2ZkNnk1NHl3NTc0NTc1Z3NoaGFG
即可得到 flag{th3_Line@r_4lgebra_1s_d1fficult!}
完。后记:最好还是用linux吧,有些库太难装了
文章仅用于普及网络安全知识,提高小伙伴的安全意识的同时介绍常见漏洞的特征等,若读者因此做出危害网络安全的行为后果自负,与合天智汇以及原作者无关,特此声明。